Chemical Reaction And Equation

Chemical Equations

As shown in Figure 4.1.1, applying a small amount of heat to a pile of orange ammonium dichromate powder results in a vigorous reaction known as the ammonium dichromate volcano. Heat, light, and gas are produced as a large pile of fluffy green chromium(III) oxide forms. This reaction is described with a chemical equation, an expression that gives the identities and quantities of the substances in a chemical reaction.

Figure 4.1.1: An Ammonium Dichromate Volcano: Change during a Chemical Reaction. The starting material is solid ammonium dichromate. A chemical reaction transforms it to solid chromium(III) oxide, depicted showing a portion of its chained structure, nitrogen gas, and water vapor (in addition, energy in the form of heat and light is released). During the reaction, the distribution of atoms changes, but the number of atoms of each element does not change. Because the numbers of each type of atom are the same in the reactants and the products, the chemical equation is balanced.

Chemical reactions are represented on paper by chemical equations. For example, hydrogen gas (H₂) can react (burn) with oxygen gas (O₂) to form water (H₂O). Thechemical equation for this reaction is written as:

2H2+O2→2H2O(4.1.1)$$\begin{array}{}\text{(4.1.1)}& 2H_2+O_2\to 2H_{2}O\end{array}$$

Chemical formulas and other symbols are used to indicate the starting materials, or reactants, which by convention are written on the left side of the equation, and the final compounds, or products, which are written on the right. An arrow points from the reactant to the products. The chemical reaction for the ammonium dichromate volcano in Figure 4.1.1 is

(NH4)2Cr2O7→Cr2O3+N2+4H2O(4.1.1)$$\begin{array}{}\text{(4.1.1)}& (N{H}_4{)}_{2}C{r}_2{O}_7\to C{r}_2{O}_3+N_2+4H_{2}O\end{array}$$

reactantproducts(4.1.2)$$\begin{array}{}\text{(4.1.2)}& reactantproducts\end{array}$$

The arrow is read as “yields” or “reacts to form.” Equation 4.1.1 indicates that ammonium dichromate (the reactant) yields chromium(III) oxide, nitrogen, and water (the products). The equation for this reaction is even more informative when written as follows:

(NH4)2Cr2O7(s)→Cr2O3(s)+N2(g)+4H2O(g)(4.1.2)$$\begin{array}{}\text{(4.1.2)}& (N{H}_4{)}_{2}C{r}_2{O}_7(s)\to C{r}_2{O}_{3(s)}+N_{2(g)}+4H_2{O}_{(g)}\end{array}$$

Equation 4.1.2 is identical to Equation 4.1.1 except for the addition of abbreviations in parentheses to indicate the physical state of each species. The abbreviations are (s) for solid, (l) for liquid, (g) for gas, and (aq) for an aqueous solution, a solution of the substance in water.

Consistent with the law of conservation of mass, the numbers of each type of atom are the same on both sides of Equations 4.1.1 and 4.1.2. Each side of the reaction has two chromium atoms, seven oxygen atoms, two nitrogen atoms, and eight hydrogen atoms.

In a balanced chemical equation, both the numbers of each type of atom and the total charge are the same on both sides.Equations 4.1.1 and 4.1.2 are balanced chemical equations. What is different on each side of the equation is how the atoms are arranged to make molecules or ions. A chemical reaction represents a change in the distribution of atoms, but not in the number of atoms. In this reaction, and in most chemical reactions, bonds are broken in the reactants (here, Cr–O and N–H bonds), and new bonds are formed to create the products (here, O–H and N≡N bonds). If the numbers of each type of atom are different on the two sides of a chemical equation, then the equation is unbalanced, and it cannot correctly describe what happens during the reaction. To proceed, the equation must first be balanced.

NOTE

A chemical reaction changes only the distribution of atoms, not the number of atoms.

Balancing Simple Chemical Equations

When a chemist encounters a new reaction, it does not usually come with a label that shows the balanced chemical equation. Instead, the chemist must identify the reactants and products and then write them in the form of a chemical equation that may or may not be balanced as first written. Consider, for example, the combustion of n-heptane (C7H16$C_7{H}_{16}$), an important component of gasoline:

C7H16(l)+O2(g)→CO2(g)+H2O(g)(4.1.3)$$\begin{array}{}\text{(4.1.3)}& C_7{H}_{16}(l)+O_2(g)\to C{O}_2(g)+H_{2}O(g)\end{array}$$

The complete combustion of any hydrocarbon with sufficient oxygen always yields carbon dioxide and water.

Figure 4.1.2: An Example of a Combustion Reaction. The wax in a candle is a high-molecular-mass hydrocarbon, which produces gaseous carbon dioxide and water vapor in a combustion reaction (see Equation 4.1.3).

Equation 4.1.3 is not balanced: the numbers of each type of atom on the reactant side of the equation (7 carbon atoms, 16 hydrogen atoms, and 2 oxygen atoms) is not the same as the numbers of each type of atom on the product side (1 carbon atom, 2 hydrogen atoms, and 3 oxygen atoms). Consequently, the coefficients of the reactants and products must be adjusted to give the same numbers of atoms of each type on both sides of the equation. Because the identities of the reactants and products are fixed, the equation cannot be balanced by changing the subscripts of the reactants or the products. To do so would change the chemical identity of the species being described, as illustrated inFigure 4.1.3.

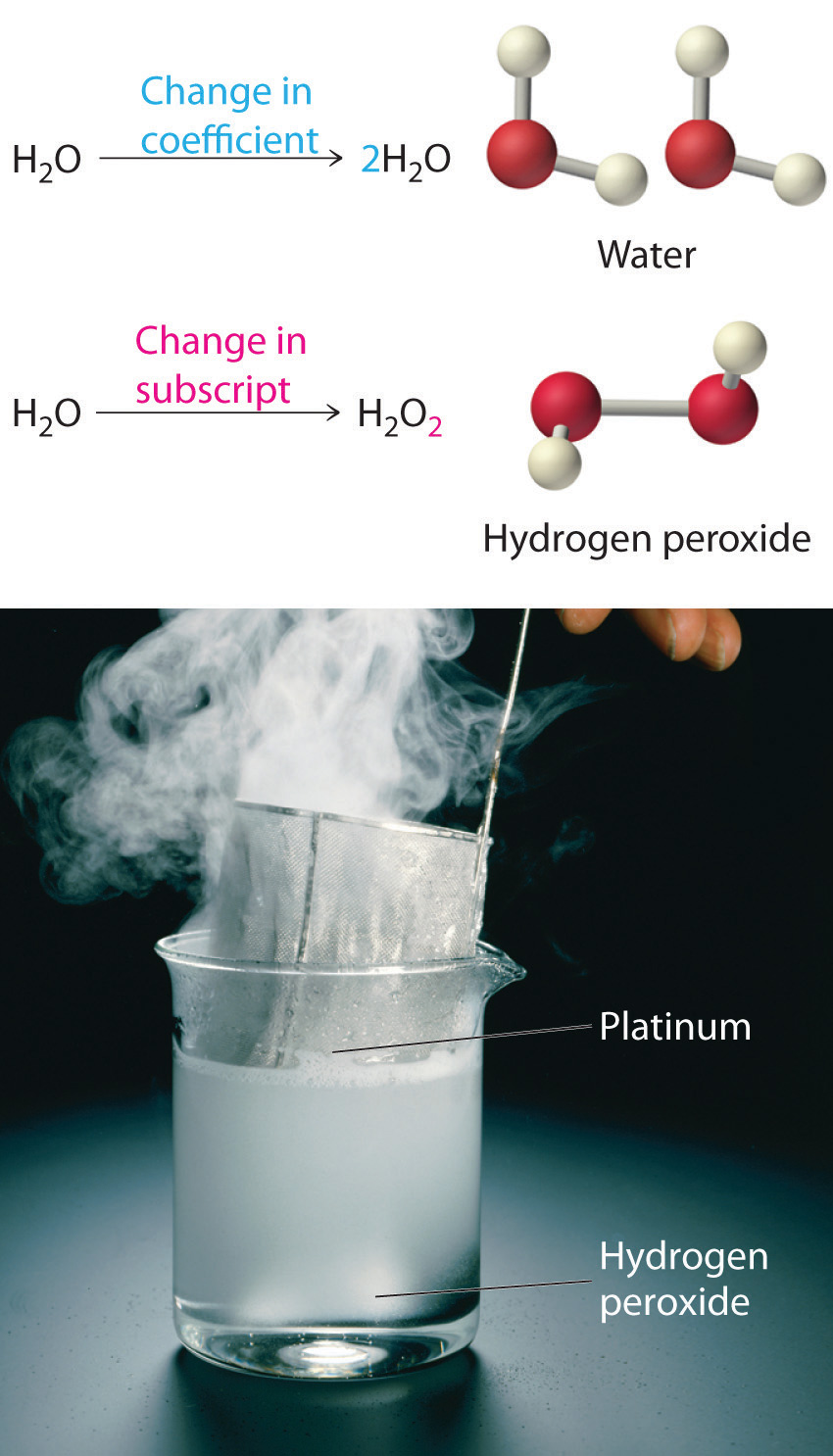
Figure 4.1.3: Balancing Equations. You cannot change subscripts in a chemical formula to balance a chemical equation; you can change only the coefficients. Changing subscripts changes the ratios of atoms in the molecule and the resulting chemical properties. For example, water (H₂O) and hydrogen peroxide (H₂O₂) are chemically distinct substances. H₂O₂decomposes to H₂O and O₂ gas when it comes in contact with the metal platinum, whereas no such reaction occurs between water and platinum.

The simplest and most generally useful method for balancing chemical equations is “inspection,” better known as trial and error. The following is an efficient approach to balancing a chemical equation using this method.

Steps in Balancing a Chemical Equation

1. Identify the most complex substance.
2. Beginning with that substance, choose an element that appears in only one reactant and one product, if possible. Adjust the coefficients to obtain the same number of atoms of this element on both sides.
3. Balance polyatomic ions (if present) as a unit.
4. Balance the remaining atoms, usually ending with the least complex substance and using fractional coefficients if necessary. If a fractional coefficient has been used, multiply both sides of the equation by the denominator to obtain whole numbers for the coefficients.
5. Count the numbers of atoms of each kind on both sides of the equation to be sure that the chemical equation is balanced.

EXAMPLE 4.1.1: COMBUSTION OF HEPTANE

To demonstrate this approach, let’s use the combustion of n-heptane (Equation 4.1.3) as an example.

1. Identify the most complex substance. The most complex substance is the one with the largest number of different atoms, which is C₇H₁₆. We will assume initially that the final balanced chemical equation contains 1 molecule or formula unit of this substance.

2. Adjust the coefficients. Try to adjust the coefficients of the molecules on the other side of the equation to obtain the same numbers of atoms on both sides. Because one molecule of n-heptane contains 7 carbon atoms, we need 7 CO₂ molecules, each of which contains 1 carbon atom, on the right side:

C7H16+O2→7CO2+H2O(4.1.4)$$\begin{array}{}\text{(4.1.4)}& C_7{H}_{16}+O_2\to 7C{O}_2+H_{2}O\end{array}$$

3. Balance polyatomic ions as a unit. There are no polyatomic ions to be considered in this reaction.

4. Balance the remaining atoms. Because one molecule of n-heptane contains 16 hydrogen atoms, we need 8 H2O molecules, each of which contains 2 hydrogen atoms, on the right side:

C7H16+O2→7CO2+8H2O(4.1.5)$$\begin{array}{}\text{(4.1.5)}& C_7{H}_{16}+O_2\to 7C{O}_2+8H_{2}O\end{array}$$

The carbon and hydrogen atoms are now balanced, but we have 22 oxygen atoms on the right side and only 2 oxygen atoms on the left. We can balance the oxygen atoms by adjusting the coefficient in front of the least complex substance, O₂, on the reactant side:

C7H16(l)+11O2(g)→7CO2(g)+8H2O(g)(4.1.6)$$\begin{array}{}\text{(4.1.6)}& C_7{H}_{16}(l)+11O_2(g)\to 7C{O}_2(g)+8H_{2}O(g)\end{array}$$

5. Check your work. The equation is now balanced, and there are no fractional coefficients: there are 7 carbon atoms, 16 hydrogen atoms, and 22 oxygen atoms on each side. Always check to be sure that a chemical equation is balanced.

The assumption that the final balanced chemical equation contains only one molecule or formula unit of the most complex substance is not always valid, but it is a good place to start. Consider, for example, a similar reaction, the combustion of isooctane (C₈H₁₈). Because the combustion of any hydrocarbon with oxygen produces carbon dioxide and water, the unbalanced chemical equation is as follows:

C8H18(l)+O2(g)→CO2(g)+H2O(g)(4.1.7)$$\begin{array}{}\text{(4.1.7)}& C_8{H}_{18}(l)+O_2(g)\to C{O}_2(g)+H_{2}O(g)\end{array}$$

1. Identify the most complex substance. Begin the balancing process by assuming that the final balanced chemical equation contains a single molecule of isooctane.

2. Adjust the coefficients. The first element that appears only once in the reactants is carbon: 8 carbon atoms in isooctane means that there must be 8 CO₂molecules in the products:

C8H18+O2→8CO2+H2O(4.1.8)$$\begin{array}{}\text{(4.1.8)}& C_8{H}_{18}+O_2\to 8C{O}_2+H_{2}O\end{array}$$

3. Balance polyatomic ions as a unit. This step does not apply to this equation.

4. Balance the remaining atoms. Eighteen hydrogen atoms in isooctane means that there must be 9 H₂O molecules in the products:

C8H18+O2→8CO2+9H2O(4.1.9)$$\begin{array}{}\text{(4.1.9)}& C_8{H}_{18}+O_2\to 8C{O}_2+9H_{2}O\end{array}$$

The carbon and hydrogen atoms are now balanced, but we have 25 oxygen atoms on the right side and only 2 oxygen atoms on the left. We can balance the least complex substance, O₂, but because there are 2 oxygen atoms per O₂ molecule, we must use a fractional coefficient (25/2) to balance the oxygen atoms:

C8H18+25/2O2→8CO2+9H2O(4.1.10)$$\begin{array}{}\text{(4.1.10)}& C_8{H}_{18}+25/2O_2\to 8C{O}_2+9H_{2}O\end{array}$$

Equation 3.18 is now balanced, but we usually write equations with whole-number coefficients. We can eliminate the fractional coefficient by multiplying all coefficients on both sides of the chemical equation by 2:

2C8H18(l)+25O2(g)→16CO2(g)+18H2O(g)(3.11)$$\begin{array}{}\text{(3.11)}& 2C_8{H}_{18}(l)+25O_2(g)\to 16C{O}_2(g)+18H_{2}O(g)\end{array}$$

5. Check your work. The balanced chemical equation has 16 carbon atoms, 36 hydrogen atoms, and 50 oxygen atoms on each side.

Balancing equations requires some practice on your part as well as some common sense. If you find yourself using very large coefficients or if you have spent several minutes without success, go back and make sure that you have written the formulas of the reactants and products correctly.